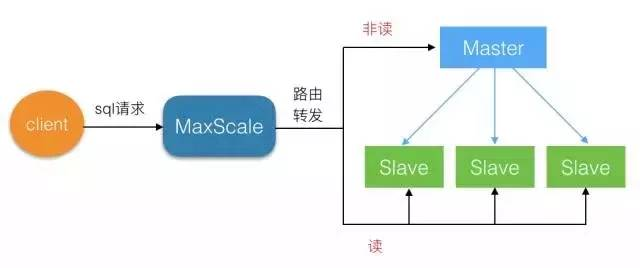
在行测数量关系中,排列组合问题因其灵活多变,往往给同学们带来很大的困扰。在排列组合中有部分题目条件较多,大家在处理的时候就需要有一定的章程,才能快速梳理出解题的思路,这就需要我们借助一定的方法。接下来,就带大家学习常用的解决排列组合问题的三大方法,大家熟练掌握这些方法后,解决排列组合问题时便能游刃有余。

 一、优限法

 题型特征:题干中有绝对限制条件的元素或者位置。

 优限法的使用:优先考虑有绝对限制条件的元素或位置,再考虑其他的元素或位置。

 【例1】一次会议某单位邀请了10名专家,该单位预定了10个房间,其中一层5间、二层5间。已知邀请专家中4人要求住二层、3人要求住一层、其余3人住任一层均可。那么要满足他们的住房要求且每人1间,有多少种不同的安排方案?

 A.75

 B.450

 C.7200

 D.43200

 答案:D。

 【解析】由题干可知,邀请的专家中有4人明确要求住二层,因此可以先考虑这4个人的住宿情况,从二层的5个房间中选4个房间安排住宿,即

接着有3人明确要求住一层,同理从一层的5个房间中选3个房间安排住宿,

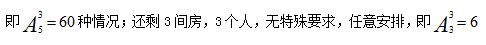
种情况;整个过程是分步完成的,因此最终结果为120×60×6=43200种情况。正确答案为D。

二、捆绑法

 题型特征:题干中要求某些元素相邻。

 捆绑法的使用:先将相邻元素捆绑成一个整体,再考虑这个整体与其他元素的顺序要求,最后考虑整体内部的顺序要求。

 【例2】一位同学买了4本不同的美术书,买了2本不同的历史书。他要把这6本书放在书架上,并且美术书都相邻,历史书也都相邻,问他有多少种不同的摆放方法?

 A.48

 B.96

 C.120

 D.720

 答案:B。

 【解析】由题干可知,同类书籍要相邻摆放,因此可以将其捆绑在一起,看做一个整体,摆放时两类书籍一共有

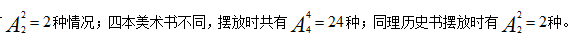
整个过程分步完成,因此最终结果为2×24×2=96种。正确答案为B。

 三、插空法

 题型特征:题干中要求某些元素不相邻。

 插空法的使用:先考虑其他元素的顺序要求,再将不相邻元素插到排好的空中。

 【例3】某单位为了丰富大家的业余生活,将8张同一排相邻的电影票发给了5个男生和3个女生,下班后这8位同事决定一同观影,若3个女生的座位互不相邻且不能在两端,问有多少种安排座位的方法?

 A.40320

 B.5040

 C.2880

 D.1440

 答案:C

 【解析】由题干可知,3个女生的座位互不相邻,因此可以先考虑男生座位的排列情况,属于5个人的全排列,

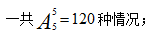
男生排好之后一共产生了6个空,但是女生的座位不能在两端,因此可供选择的位置只剩下中间4个,从4个空位中选3个将女生排列,

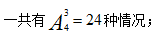
整个过程分步完成,最终结果为120×24=2880种情况。正确答案为C。

上篇： 识别关键要点巧解定义判断
下篇： 没有了